Using Algorithmic Differentiation (AD) for Enhancing Stability and Speed in Risk Computation

In the fast-paced landscape of financial engineering, accurate and efficient computation of Greeks—key sensitivities that measure risks related to changes in underlying variables—plays a crucial role in managing risk and informing trading decisions. Traditional methods, like the Bump-and-Reprice (B&R) approach, are widely used for calculating Greeks. However, with the rise of advanced modeling techniques, there’s growing interest in Algorithmic Differentiation (AD) as a more efficient, stable alternative for Greeks computation.  

In this blog, we explore the nuances of the classical B&R approach, introduce the Jacobian Greeks approach, and discuss how Numerix’s AD-based modeling framework offers significant advantages in computational speed and stability. 

The Bump-and-Reprice (B&R) Approach: A Traditional Method for Calculating Greeks 

The B&R approach is one of the most common methods for estimating Greeks, involving a simple process: the underlying variables are “bumped” by a small increment, and the instrument is repriced to observe the change. This change is used to approximate the sensitivity, or Greek, for that variable. While intuitive, this approach has limitations. It’s computationally intensive, especially for large portfolios, as each bump requires a full revaluation of the instrument. This can lead to a significant increase in computation time and potential inaccuracies, particularly for more complex instruments. 

One major drawback of B&R is its reliance on finite differences. This approximation method can create errors due to the need for small bump sizes, which can lead to instability in the Greek estimates. Additionally, when high-dimensional Greeks or path-dependent derivatives are involved, B&R becomes even more computationally costly and error-prone. 

Jacobian Greeks: An Alternative Perspective 

The Jacobian Greeks approach offers a promising alternative by leveraging the Jacobian matrix, which provides a structured way to calculate sensitivities. This method introduces a systematic framework for managing the complexities of multi-dimensional Greeks by focusing on the interrelations between underlying variables and instrument prices. The result is a more streamlined computation that avoids the instability often encountered in B&R. By treating Greeks as matrix derivatives, the Jacobian Greeks approach enables faster and more accurate sensitivity analysis, particularly for instruments with complex structures. 

This structured approach leads naturally to the integration of AD, which enhances the calculation of Jacobian Greeks through a mathematically rigorous differentiation process. 

The Numerix Modeling Framework for Algorithmic Differentiation (AD) 

Numerix’s modeling framework employs AD to offer an advanced, robust solution for Greeks computation. AD allows derivatives to be computed precisely by breaking down complex functions into a sequence of straightforward operations. These operations are then differentiated step-by-step, enabling accurate computation of derivatives without relying on approximations. 

The Numerix AD framework is designed to work seamlessly within a hybrid simulation scheme, combining forward and backward techniques to maximize efficiency. The forward scheme is used to provide the flexibility for various payoff structures while the backward scheme is used to reduce computational cost. This tailored approach leverages the strengths of each AD technique based on the specific requirements of the instrument and the types of Greeks being calculated. 

Simulation Schemes in AD: Forward and Adjoint Differentiation 

In Numerix’s hybrid framework, forward and adjoint AD schemes play complementary roles. In the forward scheme, the sensitivities need to be calculated incrementally along the simulation path. In the adjoint scheme, on the other hand, the derivatives are computed in a reverse manner after the simulation has concluded. This dual approach allows for efficient differentiation that minimizes computational load and enhances stability. 

In addition, regression derivatives are utilized within backward Monte Carlo simulations. By incorporating conditional expectations, this approach allows the model to estimate Greeks more accurately, especially for complex path-dependent derivatives. This versatility ensures that the Numerix framework can handle a broad range of instrument types and risk sensitivities with precision and efficiency. 

Comparing AD with Bump-and-Reprice: FX Example 

To illustrate the effectiveness of AD over the traditional B&R approach, consider an example involving a 6-month at-the-money call option on AUD/USD with a notional of AUD $20 million. In a model using local volatility with 30 FX Vega Greeks and 1 FX Spot Delta, the B&R method requires 63 pricing runs (for both the base and bumped scenarios) over 20,000 MC paths and 100 timesteps.  

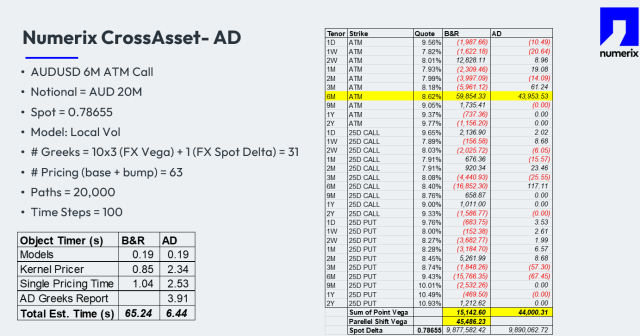
By contrast, the AD approach achieves comparable sensitivity calculations with significantly fewer computational resources, resulting in faster processing times and greater numerical stability. This example highlights the tangible advantages of AD for managing high-dimensional Greeks in a computationally efficient manner. 

The Future of Greek Computations with Algorithmic Differentiation 

As the demands of financial risk management grow, the limitations of classical approaches like B&R are becoming more evident. Leveraging AD, Numerix has developed a robust framework that addresses the computational challenges of Greek estimation. By integrating forward and adjoint differentiation techniques within a flexible, hybrid simulation scheme, Numerix’s AD framework enables faster, more accurate computation of Greeks, making it a powerful tool for modern risk managers. 

For more information and detailed examples on this topic, view our on-demand webinar: Algorithmic Differentiation for Greeks Stability and Fast Computation | Numerix